¿Quieres saber qué son los poliedros? Hemos aprendido ya mucho sobre geometría: qué son las figuras geométricas y en particular los polígonos, como así también las características de muchas otras formas geométricas planas. Pero en este caso vamos a hablar de un cuerpo geométrico, es decir de una figura geométrica con 3 dimensiones: alto, ancho y profundidad.
¿No te queda claro a qué nos estamos refiriendo? No te preocupes, porque además de aprender qué es un poliedro y de qué tipos hay, vamos a explicarte el concepto de cuerpo geométrico y de dimensión, para que te quede bien claro. En este post encontrarás además imágenes de todos los poliedros que explicaremos, ¡no te quedará ninguna duda!
ÍNDICE DE CONTENIDOS
¿Qué es un poliedro?
Los poliedros son cuerpos geométricos que tienen todas sus caras planas.
La palabra «poliedro» viene del griego, y significa «muchas caras». Todas las caras de un poliedro son polígonos.
Pero, ¿qué es un cuerpo geométrico? Un cuerpo geométrico es una figura geométrica con 3 dimensiones: alto, ancho y profundidad. Un cubo, una pirámide o una esfera son cuerpos geométricos. Un cuerpo geométrico ocupa un lugar en el espacio, y como consecuencia tiene un volumen.
¿A qué nos referimos cuando hablamos de dimensiones? Vamos a explicarlo mejor:
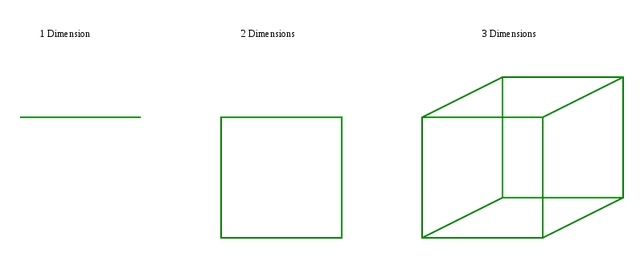
Cuando hablamos de dimensión en geometría, nos referimos al número mínimo de coordenadas que hacen falta para especificar un punto cualquiera del objeto al que nos referimos. Por ejemplo, para especificar un punto cualquiera de una línea solo hace falta una coordenada, por lo que la línea tiene una dimensión. En cambio un plano tiene dos dimensiones, porque necesitamos dos coordenadas para localizar un punto en el mismo. En cambio si queremos individuar un punto dentro de un cuerpo geométrico necesitamos 3 coordenadas, por lo que un cuerpo geométrico tiene 3 dimensiones.
RECUERDA ? Un sistema de coordenadas es un sistema que utiliza uno o más números (las coordenadas) para identificar de manera unívoca la posición de un punto u objeto geométrico. Un ejemplo sencillo son las coordenadas geográficas, que utilizan la latitud y la longitud.
Hay dos tipos de cuerpos geométricos: los cuerpos redondos o sólidos de revolución, como la esfera o el cilindro, y los poliedros, de los que nos ocupamos hoy.
Elementos de un poliedro
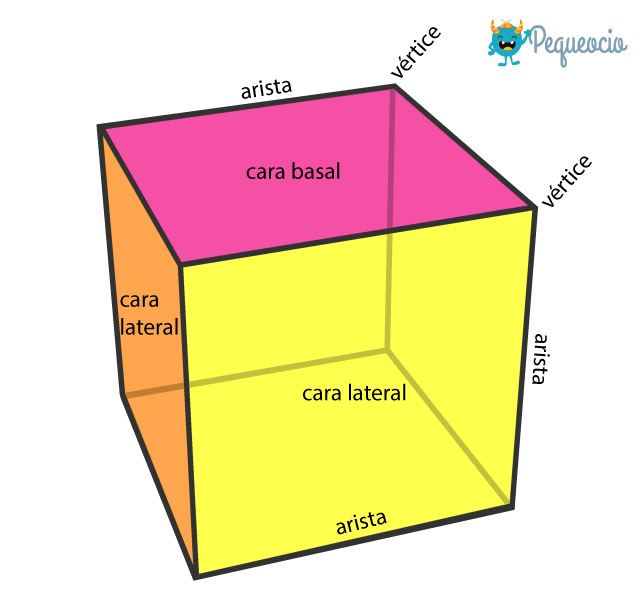
Las partes de un poliedro son:
- Cara: cada una de las superficies planas (es decir cada polígono) que delimita el poliedro.
- Arista: el segmento de línea donde se encuentran dos caras.
- Vértice: punto donde se interceptan tres o más aristas.
Tipos de poliedros
Existen diferentes modos de clasificar los poliedros. Según sus características, pueden ser:
- Convexos, cuando cualquier par de puntos del espacio que estén dentro del cuerpo los une un segmento de recta también interno. Son de este tipo todos los poliedros que veremos a continuación. O cóncavos, cuando dicho segmento se salga del cuerpo (como en el caso de una estrella tridimensional).
- Regulares, cuando todas sus caras son polígonos regulares iguales, o irregulares, cuando sus caras no son todas iguales.
Existen otros tipos de clasificaciones, pero sin duda estas son las más importantes. Estos grupos no se excluyen entre sí, es decir, un poliedro puede pertenecer a varias categorías.
Clasificación según el número de caras
| nombre | lados | nombre | lados |
| tetraedro | 4 | eneadecaedro o nonadecaedro | 19 |
| pentaedro | 5 | icosaedro o isodecaedro | 20 |
| hexaedro | 6 | triacontaedro | 30 |
| heptaedro | 7 | tetracontaedro | 40 |
| octaedro u octoedro | 8 | pentacontaedro | 50 |
| eneaedro o nonaedro | 9 | hexacontaedro | 60 |
| decaedro | 10 | heptacontaedro | 70 |
| endecaedro o undecaedro | 11 | octacontaedro u octocontaedro | 80 |
| dodecaedro | 12 | eneacontaedro o nonacontaedro | 90 |
| tridecaedro | 13 | hectaedro | 100 |
| tetradecaedro o tetracaidecaedro | 14 | chiliedro | 1000 |
| pentadecaedro o pentedecaedro | 15 | miriedro | 10000 |
| hexadecaedro | 16 | decemiriedro | 100000 |
| heptadecaedro | 17 | hectamiriedro o megaedro | 1000000 |
| octadecaedro u octodecaedro | 18 | apeiroedro | ∞ |
Poliedros regulares
Los poliedros regulares tienen todas sus caras iguales. Sus caras son todas polígonos regulares iguales, es decir que tienen todos sus lados y ángulos iguales.
Existen nueve poliedros regulares, que se dividen en dos grupos: cinco de ellos son poliedros convexos, conocidos como sólidos de Platón y los cuatro restantes son poliedros no convexos, que corresponden a la familia de los sólidos de Kepler-Poinsot.
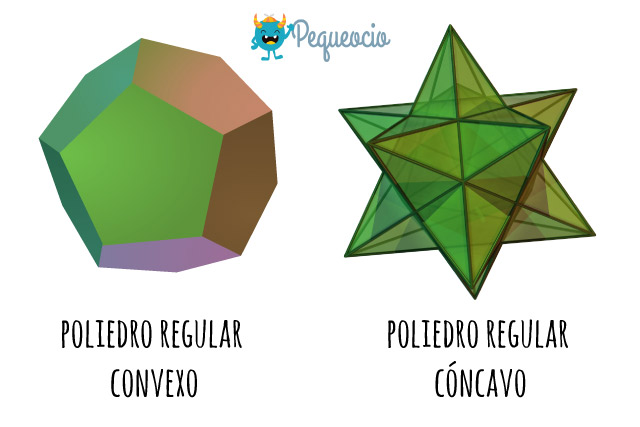
Nosotros nos ocuparemos solo de los convexos.
Tetraedro
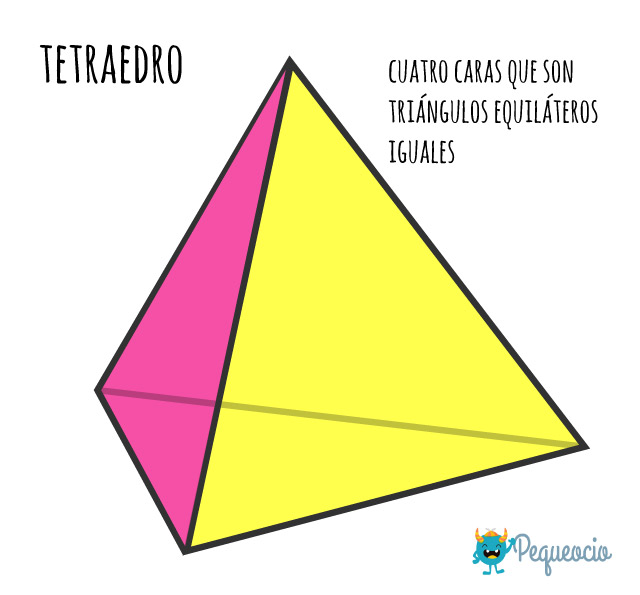
El tetraedro está compuesto por cuatro caras que son triángulos equiláteros iguales.
Un tetraedro tiene 4 vértices en los que concurren 3 caras, y 6 aristas.
Cubo
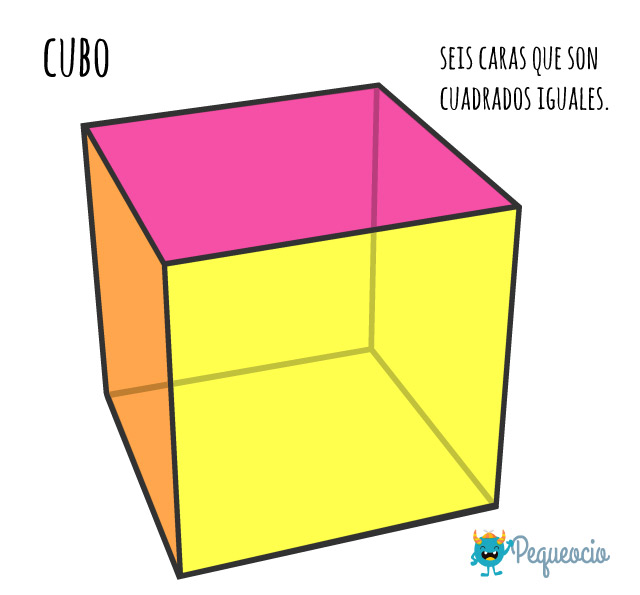
El cubo o hexaedro regular está compuestos por seis caras que son cuadrados iguales.
Tiene 8 vértices y 12 aristas.
Octaedro
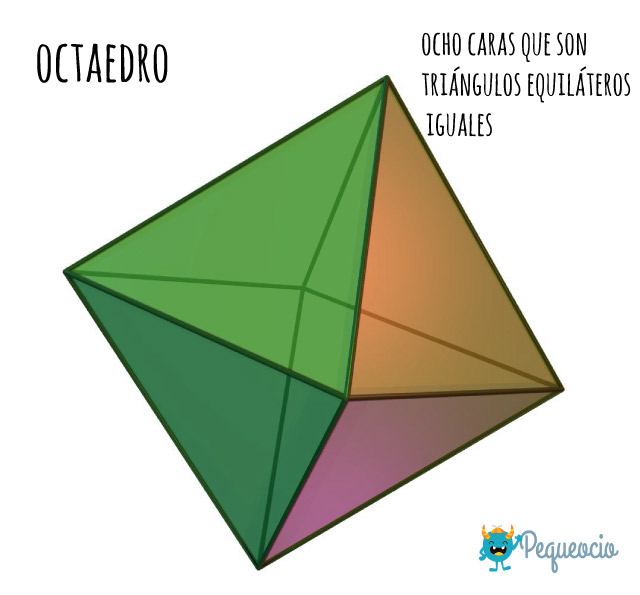
El octaedro está compuesto por ocho caras que son triángulos equiláteros iguales, en forma de dos pirámides unidas por sus bases.
Tiene 6 vértices y 12 aristas.
Dodecaedro
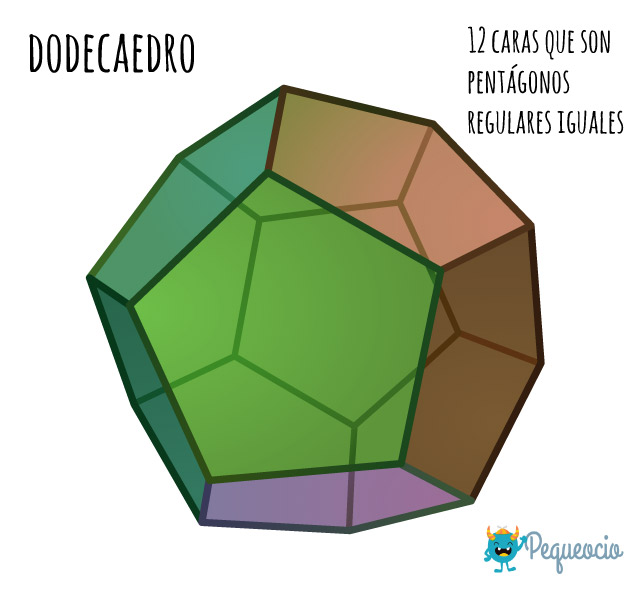
El dodecaedro está compuesto por 12 caras que son pentágonos regulares iguales.
Tiene 20 vértices y 30 aristas.
Icosaedro
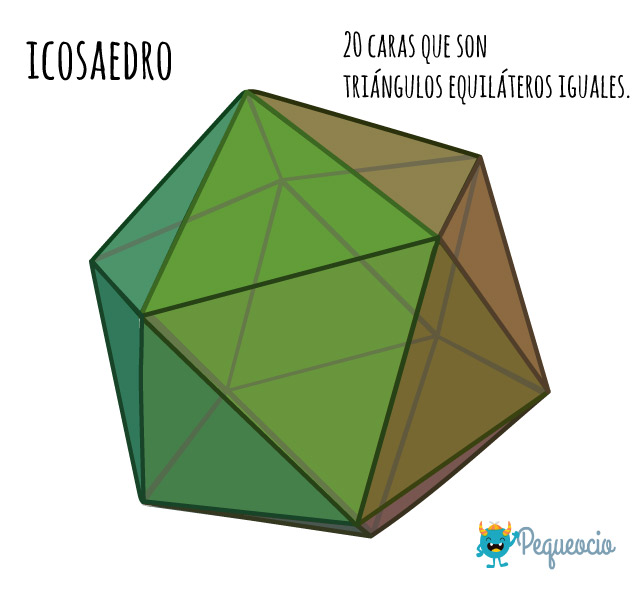
El icosaedro tiene 20 caras que son triángulos equiláteros iguales.
Cuenta con 12 vértices y 30 aristas.
Poliedros irregulares
Los poliedros irregulares son aquellos cuyas caras son polígonos que no son todos iguales.
Hay dos grandes grupos: prismas y pirámides.
Prisma
Los prismas tienen dos caras paralelas iguales, llamadas bases, y el resto de sus caras (laterales) son paralelogramos.
Podemos clasificarlos según el número de lados de las bases:
Prisma triangular
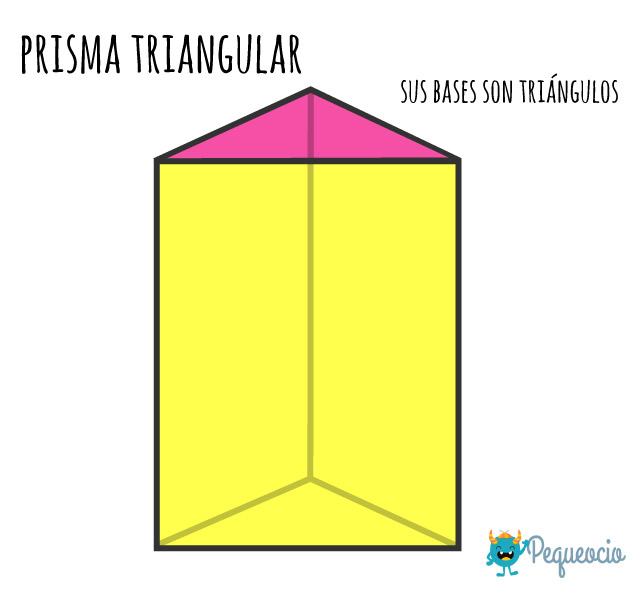
Es un prisma cuyas bases son triángulos.
Prisma cuadrangular
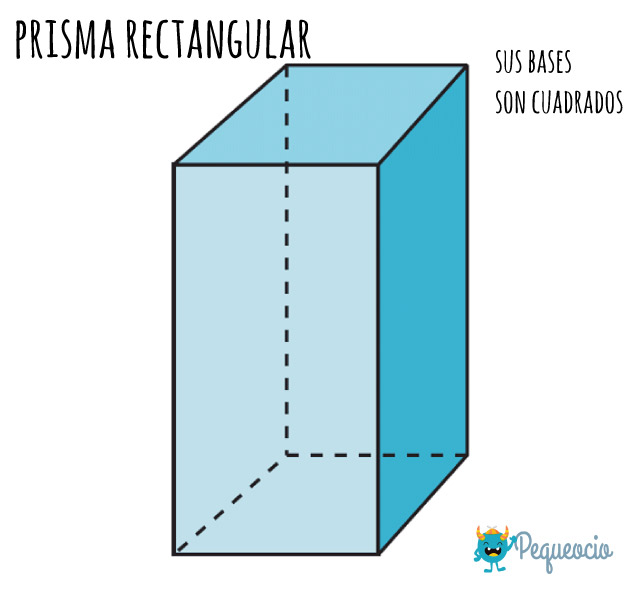
Un prisma cuadrangular es un prisma cuyas bases son cuadrados.
Prisma pentagonal
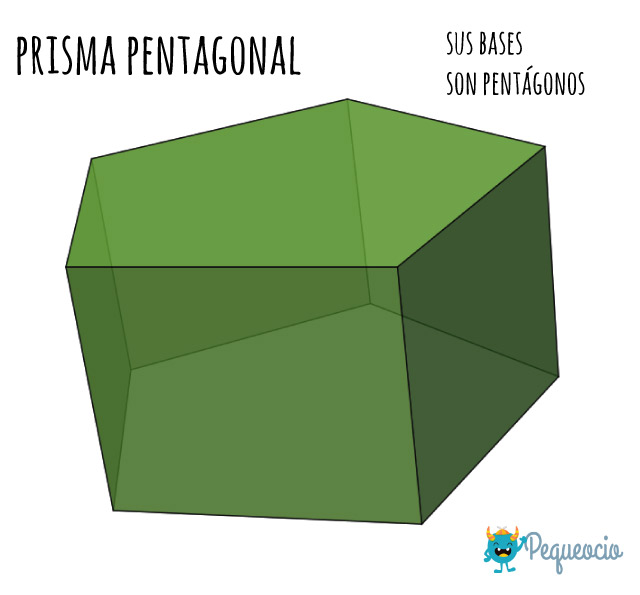
Las bases de los prismas pentagonales son pentágonos.
Prisma hexagonal
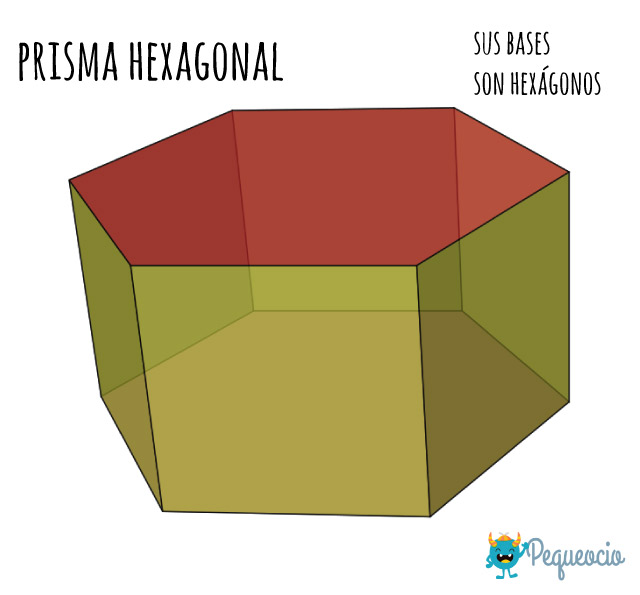
Es un prisma cuyas bases son hexágonos.
ATENCIÓN ? El prisma es recto cuando su eje es perpendicular a las bases y oblicuo cuando el ángulo entre el eje y la base es diferente a base 90°. Si el prisma es cortado de tal manera que la sección producida no sea paralela a una de sus bases, recibe el nombre de prisma truncado.
Pirámide
La pirámide es un poliedro irregular formado por una base que es un polígono cualquiera, y caras laterales triangulares que confluyen en un vértice llamado ápice, cúspide o vértice común.
La pirámide tiene tantas caras laterales como aristas tiene la base.
Pirámide triangular
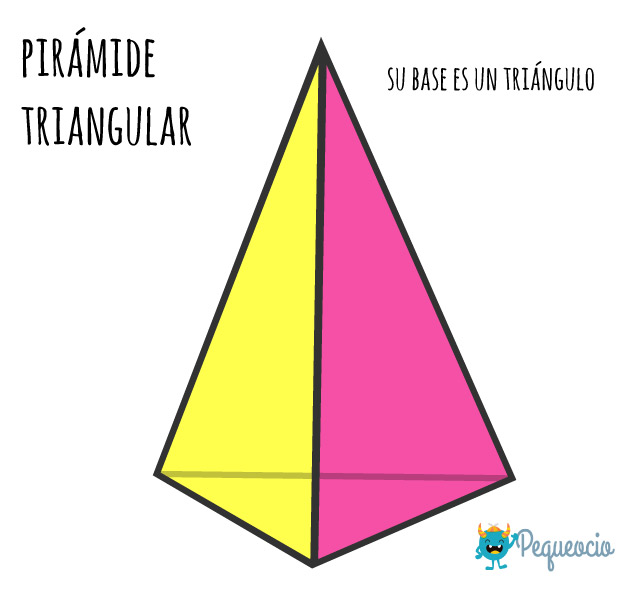
Una pirámide triangular es una pirámide que tiene un triángulo como base. Está compuesta por 4 caras: la base y 3 triángulos que confluyen en el ápice.
Pirámide cuadrangular
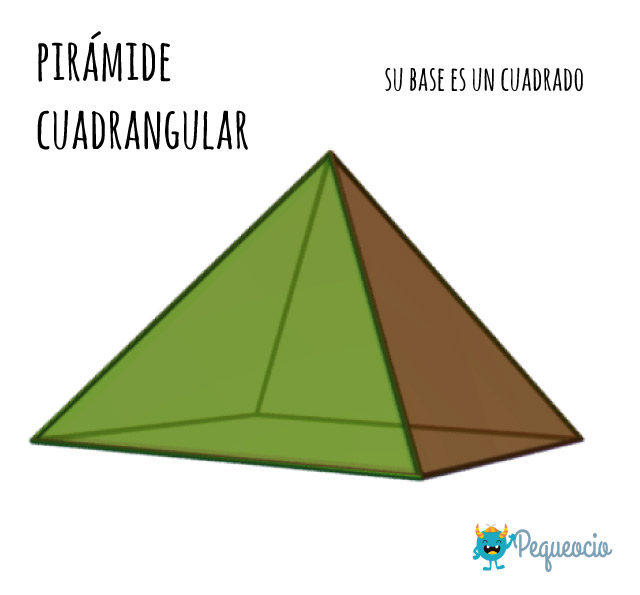
Es una pirámide cuya base es un cuadrado. Está formada por 5 caras: la base cuadrada y 4 triángulos que confluyen en el ápice.
Pirámide pentagonal
Una pirámide pentagonal es una pirámide que tiene un pentágono como base. Está formada por 6 caras: la base pentagonal y 5 triángulos que confluyen en el ápice.
Pirámide hexagonal
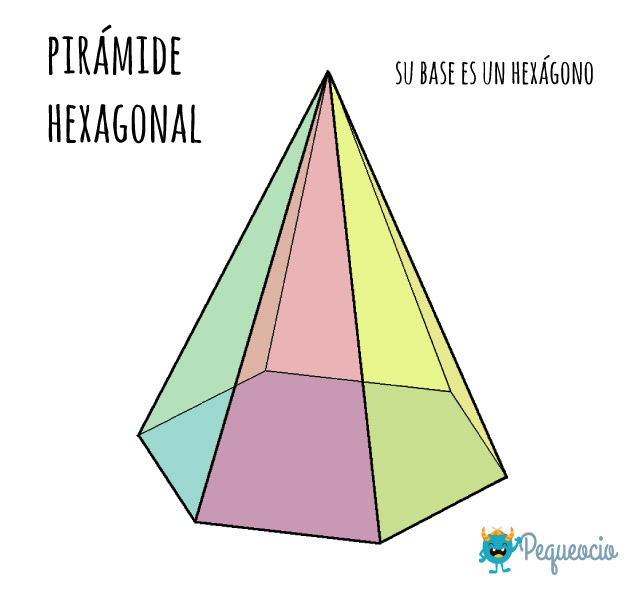
Es una pirámide con un hexágono como base. Está formada por 7 caras: la base hexagonal y 6 triángulos que confluyen en el ápice.
Tronco de pirámide
Es un poliedro irregular formado por dos caras paralelas, que son las bases, y varias caras laterales, que son trapecios. Ambas bases tienen el mismo número de lados pero una es más grande que la otra. Tiene tantas caras laterales como lados tienen las bases.
ATENCIÓN ? Cuando el eje de la pirámide es perpendicular al centro de la base, es una pirámide rectangular. En caso contrario, pirámide oblicua. Cuando un plano corta las caras laterales de la pirámide, la porción comprendida entre la base y la sección producida por dicho plano se llama tronco de la pirámide o pirámide truncada.
¿Qué te parece? Hasta aquí llegamos con nuestra clase exhaustiva sobre los poliedros.
.Png){kind=link}
