Calcular el área del cuadrado es muy sencillo, como para el resto de los paralelogramos. En este post te vamos a explicar cómo se calcula a partir de la medida de sus lados, el modo más sencillo, pero también veremos cómo calcularla a partir de la diagonal y a partir del perímetro.
Como hacemos siempre, vamos a explicarlo usando imágenes y ejemplos, para que te resulte más sencillo.
¿Qué es un cuadrado?
Antes de comenzar a ver las fórmulas, es útil repasar la definición de lo que es un cuadrado:
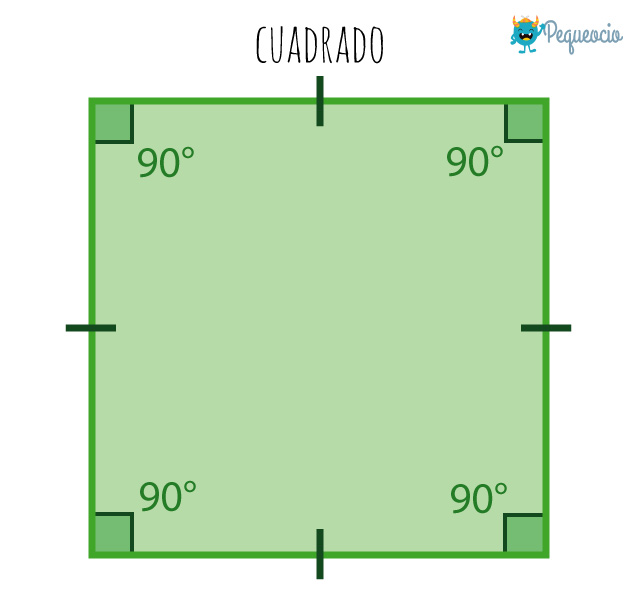
Un cuadrado es un cuadrilátero que tiene los cuatro lados iguales, y sus cuatro ángulos interiores rectos.
Sus diagonales son iguales y perpendiculares entre sí, tiene una circunferencia inscrita (la circunferencia más grande contenida en el polígono) y otra circunscrita (que pasa por todos los vértices de un polígono y contiene completamente a dicha figura en su interior).
Cómo se calcula el área de un cuadrado
Ahora sí podemos ver las fórmulas para calcular el área, pero ¿te acuerdas qué es?
el área es la superficie comprendida dentro de un perímetro, que se expresa en unidades de medidas que son conocidas como superficiales (cm2, m2, etc.)
Fórmula para calcular el área del cuadrado
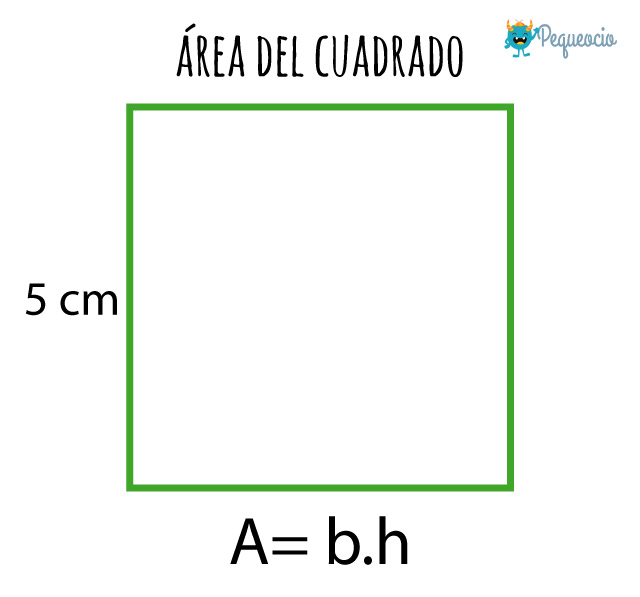
El modo más sencillo es utilizar la fórmula del área del paralelogramo, que se aplica a todas sus variantes, como el cuadrado. Para ello necesitamos saber la altura (h) y la base (b) del cuadrado; pero como sabemos que un cuadrado tiene sus cuatro lados iguales, nos alcanza conocer la medida de uno de sus lados.
Debemos multiplicar la altura (h) por la base (b), y así obtendremos la medida del área (A).
Veamos un ejemplo con un cuadrado de 5 cm de lado:
A = b . h
A = 5cm . 5cm
A= 25 cm²
Calcular el área a partir de la diagonal
La segunda forma es más compleja, porque tenemos que conocer el teorema de Pitágoras. Recordemos que este teorema relaciona los catetos de un triángulo rectángulo con su hipotenusa. Un triángulo rectángulo tiene un ángulo recto de 90° y dos ángulos menores (< 90°). Los dos lados que forman el ángulo recto son los catetos. El lado mayor opuesto al ángulo recto es la hipotenusa. El teorema de Pitágoras enuncia que:
Todos los triángulos rectángulos cumplen que la hipotenusa al cuadrado es igual a la suma de los catetos al cuadrado.
Es decir:
c² = a² + b²
Siendo a y b los dos catetos, y c la hipotenusa.
Como un cuadrado tiene cuatro ángulos rectos, la diagonal que lo corte creará un triángulo rectángulo, y así podremos aplicar el teorema de Pitágoras. Para ello necesitamos conocer la medida de la diagonal.
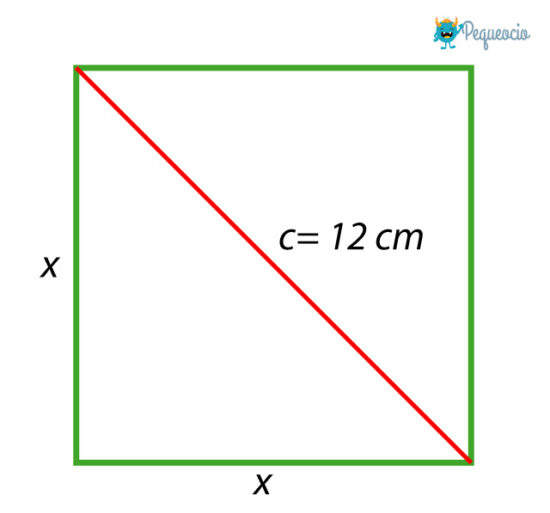
Digamos que tenemos un cuadrado con una diagonal de 12 cm:
La diagonal es la hipotenusa del triángulo (c). No conocemos la medida de los dos catetos del triángulo, pero como sabemos que los lados de un cuadrado son todos iguales, podemos identificar a ambos con la x. Ya podemos aplicar el teorema para conocer la medida de los lados del cuadrado:
Tenemos la fórmula del teorema
c² = a² + b²
Vamos a reemplazar los datos que conocemos:
12² = x² + x²
12² es igual a 144; x² por x² es igual a 2x²:
144 = 2x²
Para despejar la x, el 2 que está multiplicando lo pasamos hacia el otro lado dividiendo; 144:2 es igual a 72:
72 = x²
Quitamos el cuadrado aplicando raíz cuadrada:
√72 = √x²
x = √72 = 8,48cm
El lado del cuadrado mide 8,48 cm. Ahora podemos aplicar la fórmula del área del cuadrado, es decir
A = b . h
A = 8.48cm . 8.48cm
A = 71.91cm²
Calcular el área a partir del perímetro
Calcular el área del cuadrado a partir del perímetro es muy sencillo, porque recordemos que el perímetro es la suma de todos los lados. Por lo tanto, dado que el cuadrado tiene 4 lados iguales, solo tenemos que dividir la medida del perímetro por 4 para conocer la medida de uno de los lados.
Supongamos que tenemos un cuadrado de 20 cm de perímetro:
20cm : 4 = 5 cm
El lado del cuadrado mide 5 cm. Ahora podemos aplicar la fórmula A = b . h
A = 5cm . 5cm
A = 25cm²
¿Os ha quedado claro? Sigue aprendiendo con nosotros:
¿De cuánta utilidad te ha parecido este contenido?
¡Haz clic en las estrellas para puntuarlo!
Promedio de puntuación 4.5 / 5. Recuento de votos: 8
Hasta ahora, ¡no hay votos!. Sé el primero en puntuar este contenido.
¡Siento que este contenido no te haya sido útil!
¡Déjanose mejorar este contenido!
Dime, ¿cómo podemos mejorar este contenido?