¿Vamos a aprender todo sobre los números decimales? ¡Sí, esos que van detrás de la coma! Cuando queremos expresar un número que es menor que la unidad, tenemos que usar un decimal. Lo vamos a explicar bien sencillo, este es un artículo sobre los números decimales para primaria.
Así que comenzaremos desde el principio, explicando en qué consisten, con gráficos que te ayudarán a comprender mejor. Luego pasaremos a explicar las operaciones con decimales.
ÍNDICE DE CONTENIDOS
¿Qué son los números decimales?
Los números decimales son números no enteros, es decir que tienen una parte que es menor que la unidad. Cada número decimal tiene una parte entera y una parte decimal que va separada por una coma.
La parte decimal de los valores decimales se escribe a la derecha de la coma que la separa de las unidades:
Si dividimos el número entero, es decir la unidad, en 10 partes, tendremos 1o décimas. Si lo dividimos en 100 partes tendremos 100 centésimas. Y si lo dividimos en mil, 1000 milésimas. Vamos a verlo en este ejemplo gráfico:
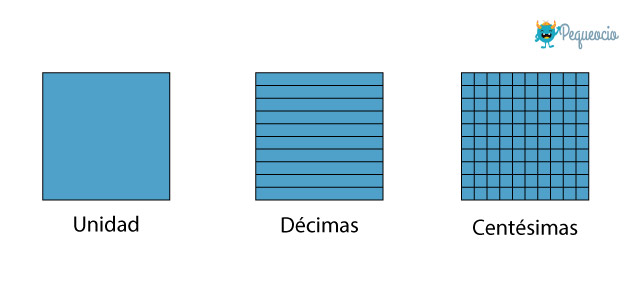
Vamos a ver unos ejemplos:
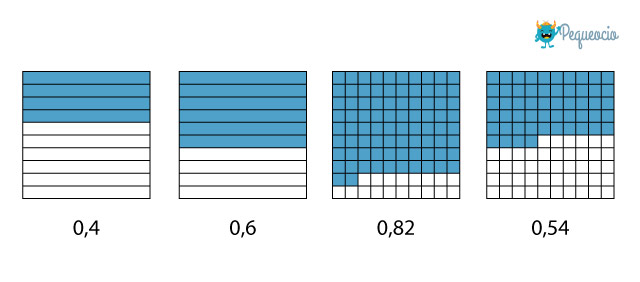
- En el primer cuadrado tenemos la unidad dividida en 10 partes iguales, por lo tanto décimas. Hemos coloreado solo 4 de estas partes. Entonces tenemos 0 unidades y 4 décimas = 0,4.
- Segundo cuadrado: lo hemos dividido en 10 partes y hemos coloreado 6. Por lo tanto tenemos 0 unidades y 6 décimas = 0,6.
- En el tercer cuadrado hemos dividido la unidad en 100 partes, por lo que tenemos centésimas. Hemos coloreado 82 partes. Significa que tenemos 0 unidades y 82 centésimas, que es lo mismo que decir 0 unidades, 8 décimas y 2 centésimas = 0,82.
- Último cuadrado: tomamos 54 partes de las 100 en las que hemos dividido la unidad. Tenemos 0 unidades, 5 décimas y 4 centésimas= 0,54.
¿Y en este caso?
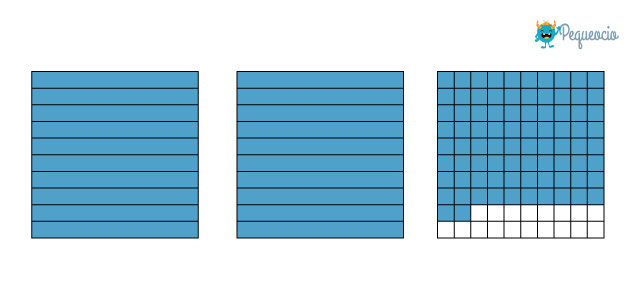
Tenemos 2 unidades y 82 centésimas = 2,82.
Tal vez todo esto que hemos explicado hasta ahora te recuerde lo que aprendimos con las fracciones (puedes repasarlo aquí). Y es que una fracción representa el número de partes que tomamos de una unidad dividida en partes iguales. Y es que los números decimales y las fracciones están relacionados. Vamos a verlo
Relación entre números decimales y fracciones
- La unidad se representa por 1.
- La décima es la unidad dividida en 10 partes iguales. Por lo tanto la fracción 1/10 es equivalente a 0,1.
- La centésima es la unidad dividida en 100 partes iguales. Por lo tanto la fracción 1/100 es equivalente a 0,01.
- La milésima es la unidad dividida en 1000 partes iguales. Por lo tanto la fracción 1/1000 es equivalente a 0,001.
Clasificación de los números decimales
Existen varios tipos de números decimales, vamos a verlos:
- exactos: son los números cuya parte decimal tiene una cantidad limitada de cifras decimales: 3,765; 48,79685.
- periódicos: son los que tienen un número ilimitado o infinito de cifras decimales, pero que tienen un patrón que se repite. Como no podemos escribir las cifras decimales al infinito, se ponen tres puntos a continuación de las cifras decimales que componen el patrón que se repite: 23, 33…; 56,879879…
- no periódicos: son los que tienen un número ilimitado o infinito de cifras decimales que no siguen ningún patrón.
Operaciones con números decimales
Suma y resta
Para sumar y restar decimales tenemos que encolumnar los números de la operación alineando las unidades con las unidades, las decenas con las decenas, etc. Si sumamos dos números que no tienen la misma cantidad de decimales, vamos a agregar 0 a la derecha hasta igualarlos:
23,54 + 48,567
23,540 + 48,567
Luego procedemos a hacer la suma o la resta por columnas, del mismo modo que se hace con los números enteros (repasa las sumas y restas). En el resultado ponemos la coma en el mismo lugar en el que está en los números que hemos sumado o restado.
Multiplicación
Para multiplicar números decimales, debemos resolver la multiplicación sin tener en cuenta la coma. La cantidad de cifras decimales del resultado será la suma de las cifras decimales de los números multiplicados. Por ejemplo, en la operación 3,28 x 4,56 tenemos un total de 4 cifras decimales (dos en cada número). El resultado sin tener en cuenta la coma es 149568. Ponemos la coma contando 4 cifras desde la derecha (para que nos queden 4 decimales), el resultado es 14,9568.
División
En el caso de la división, se dan diferentes casos, según el número con decimales sea el dividendo, el divisor o ambos.
Dividendo decimal
Se divide sin tener en cuenta la coma, y cuando se llega a bajar el número que sigue a la coma, se pone en el mismo lugar en el resultado y se sigue dividiendo:
34,56 / 8 = 4, 32
Divisor decimal
Para dividir con el divisor decimal y el dividendo entero, debemos correr la coma del divisor hacia la derecha hasta el final del número, y agregar la misma cantidad de 0 a la derecha del divisor:
- si tenemos que dividir 345 / 4,653 movemos la coma del divisor hasta después del 3, es decir 3 posiciones (la décima 6, la centésima 5 y la milésima 3). Es lo mismo que multiplicarlo por 1000.
- Por lo tanto debemos agregar tres 0 al dividendo (345000), que es siempre multiplicarlo por 1000.
- Ahora tenemos ambos números sin comas para hacer la operación: 345000 / 4653
- Haciendo esto obtendremos una división equivalente, por lo que cociente (es decir el resultado) será el mismo. Solo el resto será diferente, porque al igual que las cifras originales ha sido multiplicado por 1000. Para obtener el resto de la división original, tenemos que dividirlo por 1000.
Dividendo y divisor decimal
Tenemos que hacer lo mismo que en el ejemplo anterior, solo que debemos escoger el número que tenga más decimales. Si tenemos que dividir 45,7 / 3,28, el que tiene más decimales es el divisor (3,28) por lo que multiplicaremos ambos por 100 (o moveremos la coma dos lugares hacia la derecha, que es lo mismo). Ahora con los dos números sin comas (4570 /328) podemos proceder con la división.
¿Te ha quedado claro? No te olvides que en nuestra sección de Educación tenemos un montón de recursos para el cole.
Sigue aprendiendo con nosotros:
