Estudiando geometría nos topamos de inmediato con términos como bisectriz, mediatriz, etc… Ya lo hemos visto cuando hablamos de triángulos, y hoy vamos a dedicarnos especialmente a las bisectrices, para que te quede muy claro qué son, cuáles son sus propiedades y cómo dibujar la bisectriz de un ángulo, algo que seguro tendrás que hacer en el cole.
ÍNDICE DE CONTENIDOS
Qué es la bisectriz
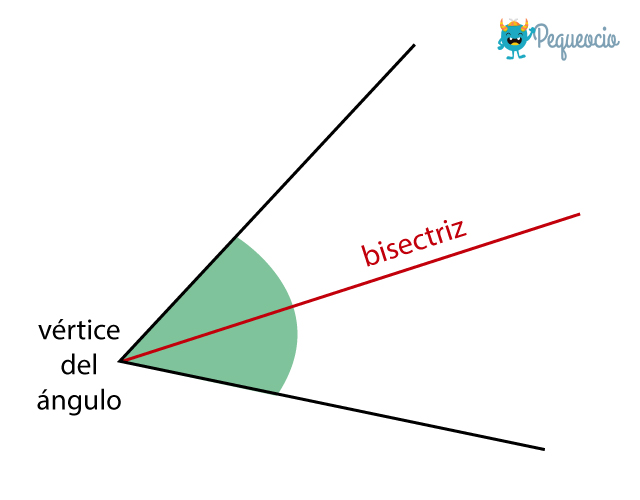
La bisectriz de un ángulo es la recta que pasando por el vértice del ángulo, lo divide en dos ángulos iguales.
¿La definición no te ha quedado del todo clara? Lo vas a entender perfectamente con este dibujo:
Propiedades de la bisectriz
- La bisectriz es el eje de simetría de un ángulo, porque sus puntos son equidistantes (están a la misma distancia) a los dos lados del ángulo.
- Dos rectas, al intersecarse, determinan cuatro ángulos. Sus bisectrices, que pasan por el punto de intersección, forman cuatro ángulos rectos.
Bisectrices de un triángulo
En el caso de los triángulos, las bisectrices tienen propiedades particulares, según el tipo de triángulo del que se trate:
Triángulo isósceles
- Cualquier triángulo con dos bisectrices de igual longitud es isósceles. Esta proposición es conocida como el teorema de Steiner-Lehmus.
- En un triángulo isósceles la mediatriz de su base (línea recta perpendicular a la base trazada por su punto medio) es eje de simetría, porque es también bisectriz.
- La recta que es trazada desde el vértice opuesto a la base hasta el punto medio de la base del triángulo isósceles, es a la vez la altura, la mediana y la mediatriz, así como también la bisectriz relativa al ángulo opuesto de la base.
Aprende más sobre el triángulo isósceles
Triángulo equilátero
- Cada altura ( recta que va desde el vértice hasta el lado que es opuesto y además esta recta es perpendicular a dicho lado), mediana (recta que parte desde el punto medio de un lado, y llega al vértice opuesto), bisectriz, mediatriz y eje de simetría de un triángulo equilátero coinciden sobre una misma recta.
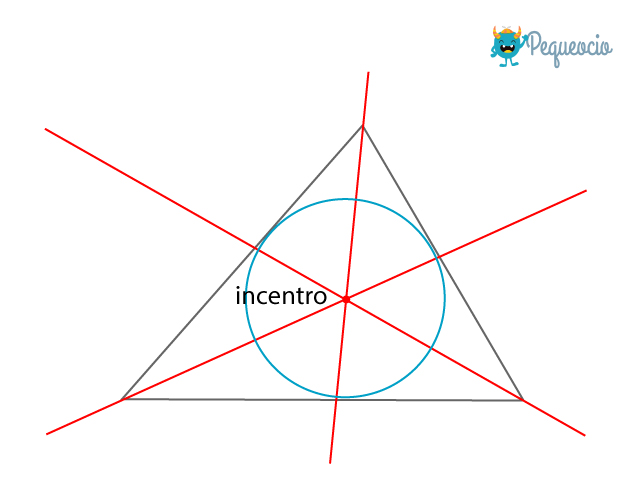
? Las tres bisectrices de los ángulos internos de un triángulo se cortan en un único punto, que equidista (está a la misma distancia) de los lados. Este punto se llama el incentro del triángulo y es el centro de la circunferencia inscrita al triángulo. Esta circunferencia es tangente (que toca pero sin llegar a cortar) a cada uno de los lados del triángulo.
Cómo dibujar una bisectriz
El método para dibujar la bisectriz de un ángulo es sencillo. Solo necesitas un compás y una regla, y por supuesto un lápiz. No importa la amplitud del ángulo, el método siempre es el mismo:
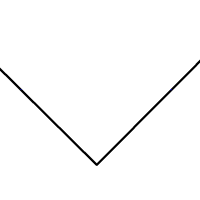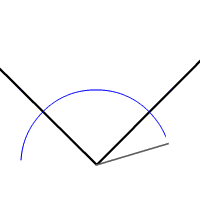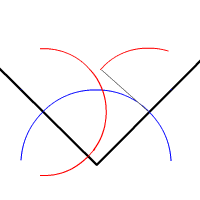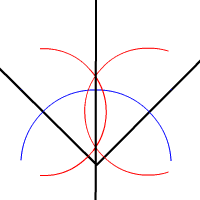
- Pon la punta de tu compás en el vértice del ángulo y traza una circunferencia de cualquier medida.
- Ahora pon la punta del compás en el punto de intersección de la circunferencia con uno de los lados, y traza una nueva circunferencia (de preferencia más pequeña).
- Repite la operación poniendo la punta del compás en la intersección de la circunferencia con el otro lado, trazando una circunferencia igual a la anterior (es decir sin abrir o cerrar el compás).
- Ahora con la regla traza una línea desde el vértice del ángulo hasta el o los puntos de intersección de las dos circunferencias iguales que trazaste en los puntos 2 y 3: acabas de dibujar la bisectriz del ángulo.
¡Ya has aprendido todo sobre la bisectriz! Sigue aprendiendo geometría con nosotros:
Imagen principal www.freepik.com