El perímetro es uno de los conceptos bases de la geometría, cuando nos referimos a figuras planas. Calcular el perímetro de cualquier forma geométrica plana es bastante sencillo, si conoces la fórmula.
A continuación te vamos a explicar cómo se calcula, con la fórmula paso a paso de todas las formas geométricas.
ÍNDICE DE CONTENIDOS
¿Qué es el perímetro?
El perímetro es la suma de las longitudes de la o las líneas que forman el contorno de una figura geométrica plana, es decir de sus lados.
Podríamos decir que el perímetro es la frontera de la figura geométrica; mientras que el área es la medida de su superficie interior.
Calcular perímetro de los polígonos
Los polígonos son figuras geométricas planas compuestas por una secuencia finita de segmentos rectos consecutivos que encierran una región en el plano. Estos segmentos son llamados lados. El perímetro de un polígono es la suma de las longitudes de todos sus lados. Vamos a ver en particular los polígonos más simples: cuadrado, rectángulo y triángulo.
Ver los cuadriláteros
Perímetro de un cuadrado
No hay nada más fácil que calcular el perímetro del cuadrado. Sabemos que un cuadrado tiene cuatro lados iguales, por lo tanto es tan sencillo como multiplicar por 4 la longitud de uno de sus lados:
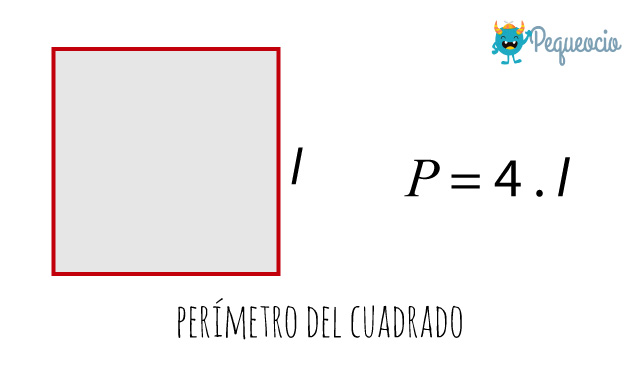
Ejemplo
Vamos a calcular el perímetro (P) de un cuadrado de 6 cm de lado:
P = 4 . 6
P = 24 cm
ATENCIÓN ? Esta fórmula también es válida para el rombo, porque tiene los cuatro lados iguales.
Perímetro de un rectángulo
Para calcular el perímetro del rectángulo tenemos que recordar que tiene dos pares de lados iguales, por lo tanto vamos a sumar la longitud de dos lados diferentes (la altura y la base), y multiplicar el resultado por 2:
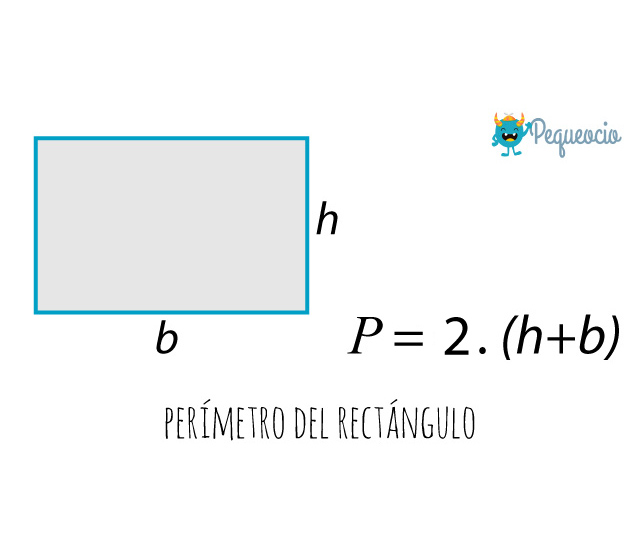
Ejemplo
Tenemos un rectángulo de 7 cm de base por 5 de altura:
P = 2 . (7+5)
P = 2 . 12
P = 24 cm
ATENCIÓN ? Esta fórmula también es válida para el romboide (paralelogramo que tiene lados contiguos desiguales y no tiene ángulos rectos)
Perímetro de un triángulo
Para calcular el perímetro del triángulo tenemos que saber qué tipo de triángulo es: equilátero, escaleno o isósceles.
Triángulo equilátero
Tiene sus tres lados iguales, por lo que solo tenemos que multiplicar la longitud de un lado por 3:
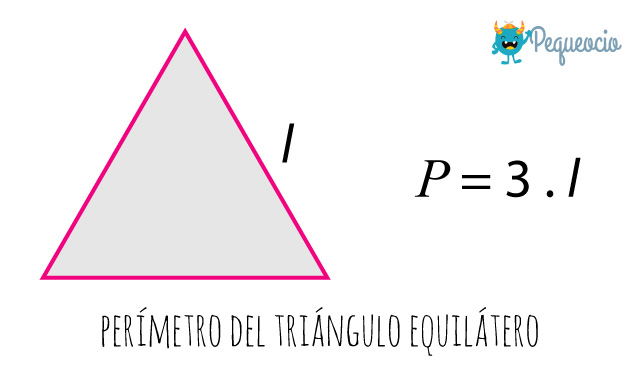
Ejemplo
Tenemos un triángulo equilátero de 7 cm de lado:
P = 3 . 7
P = 21 cm
SIGUE APRENDIENDO SOBRE EL TRIÁNGULO EQUILÁTERO
Triángulo isósceles
El isósceles tiene dos lados de igual longitud, mientras que el tercero es diferente. Por lo tanto tenemos que multiplicar la longitud de uno de los lados iguales por 2, y sumarle la longitud del lado desigual:
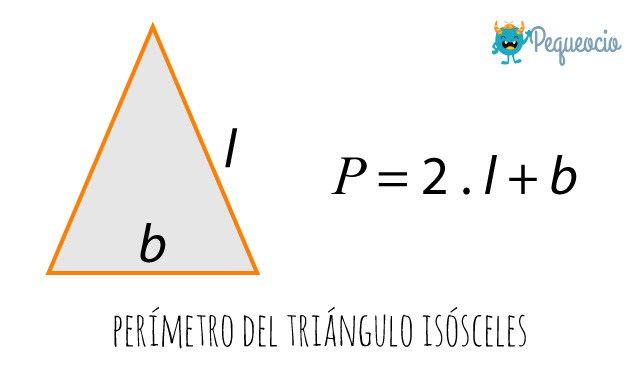
Ejemplo
Tenemos un triángulo isósceles con dos lados de 10 cm y un lado de 6 cm:
P = 2 . 10 + 6
P = 20 + 6
P = 26 cm
SIGUE APRENDIENDO SOBRE EL TRIÁNGULO ISÓSCELES
Triángulo escaleno
El triángulo escaleno es el que tiene los tres lados diferentes. Así que solo tendremos que sumarlos:
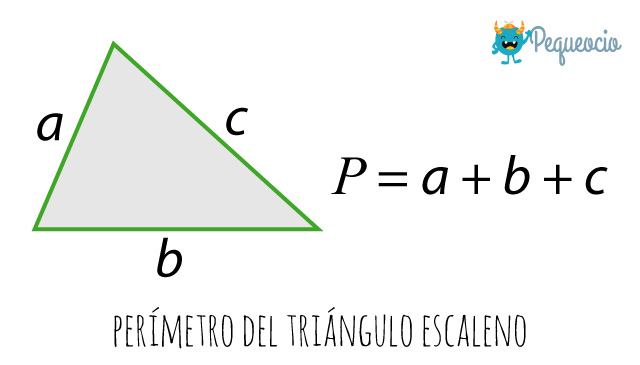
Ejemplo
Tenemos un triángulo cuyos lados miden 5, 7 y 8 cm:
P = a + b + c
P = 5 + 7 + 8
P = 20 cm
Perímetro de una circunferencia
La circunferencia es la línea curva cerrada que delimita al círculo. Por lo tanto el perímetro de un círculo es igual a la longitud de su circunferencia.
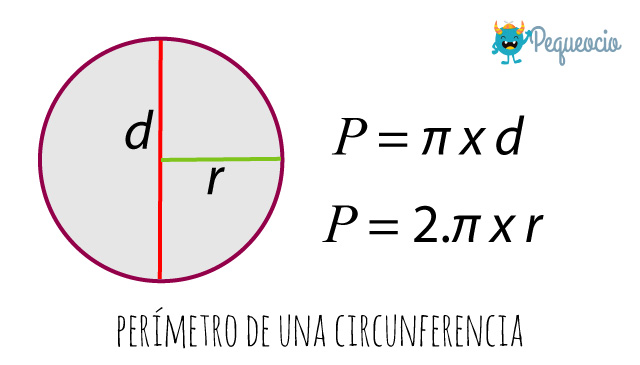
Tenemos dos fórmulas posibles para calcularlo:
- Multiplicando PI (π) por el diámetro (d): P =π x d
- Multiplicando dos veces PI (π) por el radio (r): P = 2π x r
RECUERDA ? El número PI, cuyo símbolo es π, es la relación entre la longitud de una circunferencia y su diámetro. Es decir, las veces que el diámetro entra en la circunferencia. Es un número constante, porque no importa cuál sea la circunferencia del círculo, el número π será siempre el mismo. Tiene un número indefinido de decimales (actualmente se han calculado dos billones y medio), pero para realizar cálculos matemáticos se utilizan cuatro: π = 3.1416
Ejemplo
Si tenemos un círculo de 5 cm de diámetro, y por lo tanto de 2,5 cm de radio, el resultado es el siguiente usando la primera fórmula:
P =π x d
P = 3.1416 x 5
P = 15,708 cm
Si usamos la segunda fórmula:
P = 2π x r
P = 2(3.1416) x 2.5
P = 6.2832 x 2.5
P = 15,708 cm
Hasta aquí llegamos con esta lección, ¿te ha quedado claro lo que es el perímetro?
Imagen principal freepik
Muy buenas las imágenes, pero la fórmula del perímetro en un rectángulo es 2 x (h+b), no 4, para que la puedan modificar, eso a veces puede confundir a los que están aprendiendo.
Gracias!!!
Ya lo hemos corregido, ¡muchas gracias por avisarnos del error!